结 论
先说结论,对于M-QAM调制而言,QAM符号的平均能量\(E_{s}\)可以由下式计算得到
$$E_{s}=\left(\frac{M-1}{6}\right)d^{2}$$
其中M是QAM调制的维度,d是星座图中点与点之间的最小距离,以下图的4QAM星座图为例,那么d=2。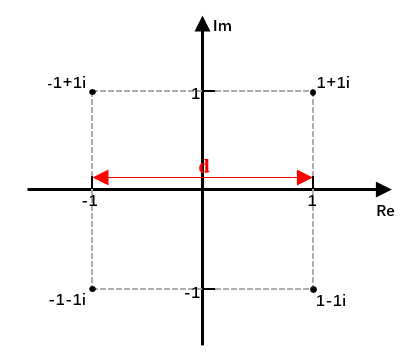
计算&推导
计算原理
先举个例子,还是以d=2的4QAM调制为例,其平均符号能量等于星座图中每个符号能量的能量之和除以星座点数
$$E_{s}=\left(\left||1+1i\right||^{2}+\left||1-1i\right||^{2}+\left||-1+1i\right||^{2}+\left||-1-1i\right||^{2}\right)/4=2$$
和结论中给出的公式计算结果\(E_{s}=\left(4-1\right)/6*2^{2}=2\)相同
由于星座图具有对称性,4个象限的符号能量是相同的,那么只需要计算其中一个象限的平均符号能量就可以得到整个星座图的平均符号能量了,比如计算第一象限,该象限内只有一个星座点,那么
$$E_{s}=\left||1+1i\right||^{2}/1=2$$
16QAM、64QAM等高阶QAM调制也同理,但是高阶调制也这么一个个求平方和会很麻烦,因此需要推导出一个通用的公式,避免用这么麻烦的方法计算平均符号能量。
推导公式
上面的计算都是以d=2为例,直接以具体的数字进行的计算,下面不代入具体的d值进行推导,4QAM、16QAM、64QAM第一象限的星座图如下所示。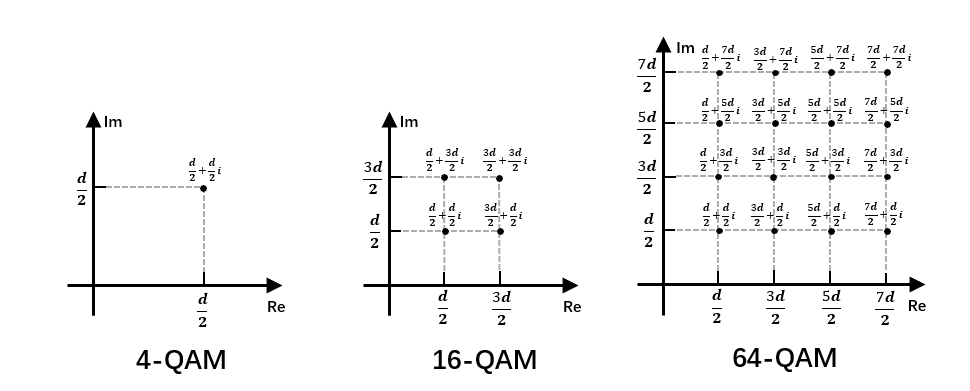
可以看出,在第一象限内4QAM的星座点坐标的实部和虚部的可能取值有\(\frac{d}{2}\),共1个点;16QAM的可能取值有\(\frac{d}{2}、\frac{3d}{2}\),共4个点;而64QAM是\(\frac{d}{2}、\frac{3d}{2}、\frac{5d}{2}、\frac{7d}{2}\),共16个点。如下表所示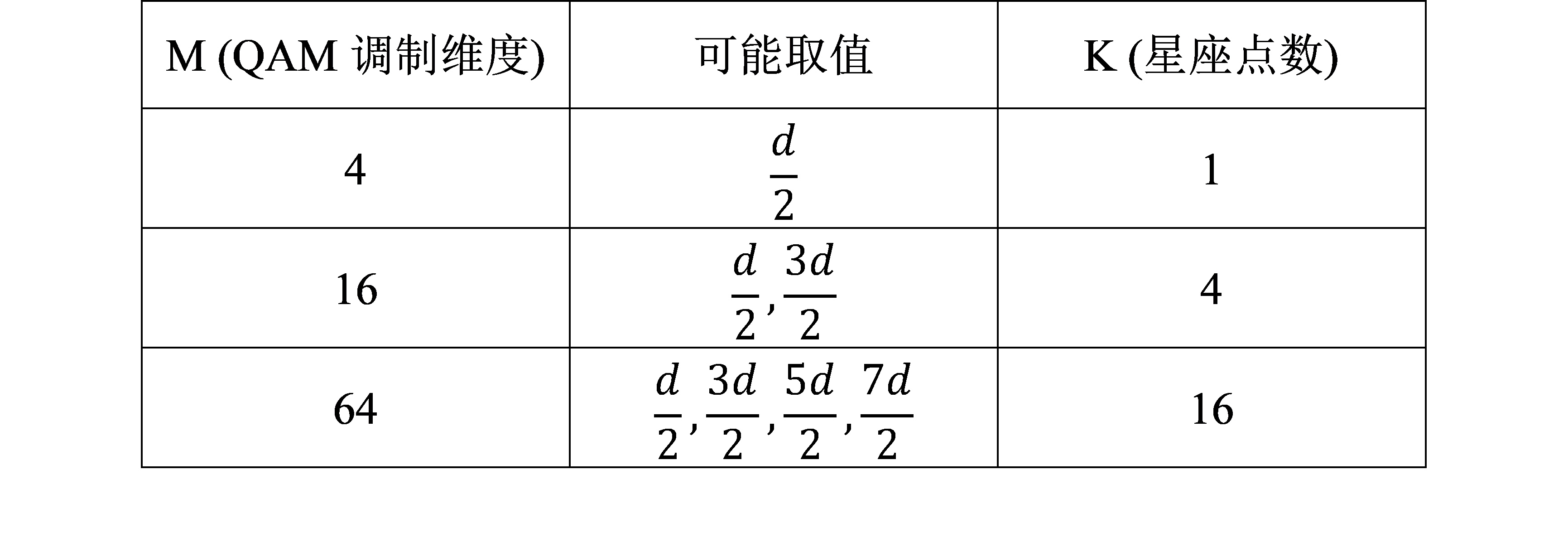
注:表中数据仅代表第一象限
下面以16QAM为例进行推导,按照计算原理可以得到16QAM的平均符号能量计算公式为
$$E_{s}=\frac{\left ( \frac{d}{2} \right )^{2}+\left ( \frac{d}{2} \right )^{2}+\left ( \frac{3d}{2} \right )^{2}+\left ( \frac{d}{2} \right )^{2}+\left ( \frac{d}{2} \right )^{2}+\left ( \frac{3d}{2} \right )^{2}+\left ( \frac{3d}{2} \right )^{2}+\left ( \frac{3d}{2} \right )^{2}}{4}$$
其每个可能取值的平方在计算中都出现了\(2\sqrt{M}\)次,那么合并同类项就可以得到
$$E_{s}=\frac{\frac{d}{2}^{2}×4+\frac{3d}{2}^{2}×4}{4}=\frac{\frac{1}{2}^{2}+\frac{3}{2}^{2}}{4}×4×d^{2}$$
对上式进行推理演绎可知对于M-QAM调制,其平均符号能量的计算式为
$$E_{s}=\frac{\frac{1}{2}^{2}+\frac{3}{2}^{2}+…+\frac{\left(\sqrt(M)-1\right)}{2}^{2}}{M/4}×2\sqrt{M}×d^{2}$$
根据数列求和的知识容易证得
$$\frac{1}{2}^{2}+\frac{3}{2}^{2}+…+\frac{2n-1}{2}^{2}=\frac{n×\left(2n-1\right)×\left(2n+1\right)}{3}$$
用\(\sqrt(M)\)替换\(2n\)就可以得到
$$\frac{1}{2}^{2}+\frac{3}{2}^{2}+…+\frac{\sqrt{M}-1}{2}^{2}=\frac{\sqrt{M}\left(M-1\right)}{6}$$
那么对于M-QAM调制而言,其平均符号能量就等于
$$E_{s}=\frac{\frac{\sqrt{M}\left(M-1\right)}{6}}{\frac{M}{4}}2\sqrt{M}d^{2}=\left(\frac{M-1}{6}\right)d^{2}$$
完。